热力学与相图计算讲座
第一讲:杠杆原理
符号
- \(x_i^{\alpha}\): \(\alpha\)相中组元\(i\)的摩尔分数
- \(w_i^{\alpha}\): \(\alpha\)相中组元\(i\)的质量分数
- \(f^{\alpha}\): \(\alpha\)相的摩尔分数
- \(f_w^{\alpha}\): \(\alpha\)相的质量分数
- \(M_i\): 组元 \(i\)的分子量
- \(m^{(j)}\): 第\(j\)个相的摩尔数
杠杆原理(Lever Rule)是帮助我们阅读理解相图的基础知识之一。它表达了在相图中一个体系的总的组成与各个相的组成之间的相对量的关系。我们的讨论对象是一个多元系的体系中的两相平衡,三相平衡和多相平衡。组成的量(amount)可以用摩尔量或质量来表示。因为在一个平衡的体系中,各个相的温度和压力都是相等的,所以这里的讨论都是在组成的空间里。我们先以摩尔量来讨论杠杆原理,然后分析摩尔量与质量之间的关系。
1. 两相平衡
设在一个由\(c\)个组元构成的\(\alpha\)-\(\beta\)两相平衡体系。体系的平均组成由体系组元的摩尔分数\(x_i^{s}\) 表示。上标\(s\)代表体系的量,下标\(i\)代表组元的序号。从质量守恒和摩尔分数归一化条件,我们有以下两个方程,
\begin{align}
&x_i^{s} = f^{\alpha} x_i^{\alpha} + f^{\beta} x_i^{\beta} \quad \quad (i=1,2,\cdots,c) \label{EQ1} \\
&f^{\alpha} + f^{\beta} = 1 \label{EQ2}
\end{align}
式(\ref{EQ1})代表组元的质量守恒,式(\ref{EQ2})表明两个相\(\alpha\)和\(\beta\)的摩尔分数\(f^{\alpha}\)和\(f^{\beta}\)满足归一化条件。摩尔分数\(f^{\alpha}\)和\(f^{\beta}\)可以从上面的公式中解出,
\begin{align}
&f^{\alpha} = \frac { x_i^{\beta}- x_i^{s}} { x_i^{\beta}- x_i^{\alpha}} \label{EQ4} \\
&f^{\beta} = \frac { x_i^{s}- x_i^{\alpha}} { x_i^{\beta}- x_i^{\alpha}} \label{EQ5}
\end{align}
如图1\((a)\)所示,体系总的组成在\(s\)点,
\(\alpha\)和\(\beta\)相的组成分别在\(\alpha\)和\(\beta\)处。\(s\)点一定是在\(\alpha\)和\(\beta\)点的联线\(\overline{\alpha \beta}\)上。\(\alpha\)和\(\beta\)相的相摩尔分数可以用线段的长度比来表示,
\begin{align}
&f^{\alpha} = \frac {\overline{s \beta}} { \overline{\alpha \beta}} \label{EQ6} \\
&f^{\beta} = \frac {\overline{\alpha s}} { \overline{\alpha \beta}} \label{EQ7}
\end{align}
图1\((b)\)把\(\alpha\)和\(\beta\)线段\(\overline{\alpha\beta}\)看作一根杠杆,支点在\(s\)点,两相的摩尔分数 \(f^\alpha\)和\(\beta\)分别就像挂在\(\alpha\)和\(\beta\)两端的质量为\(f^\alpha\)和\(f^\beta\)的重物,此杠杆系统达到平衡状态。这就是两相平衡的杠杆原理。
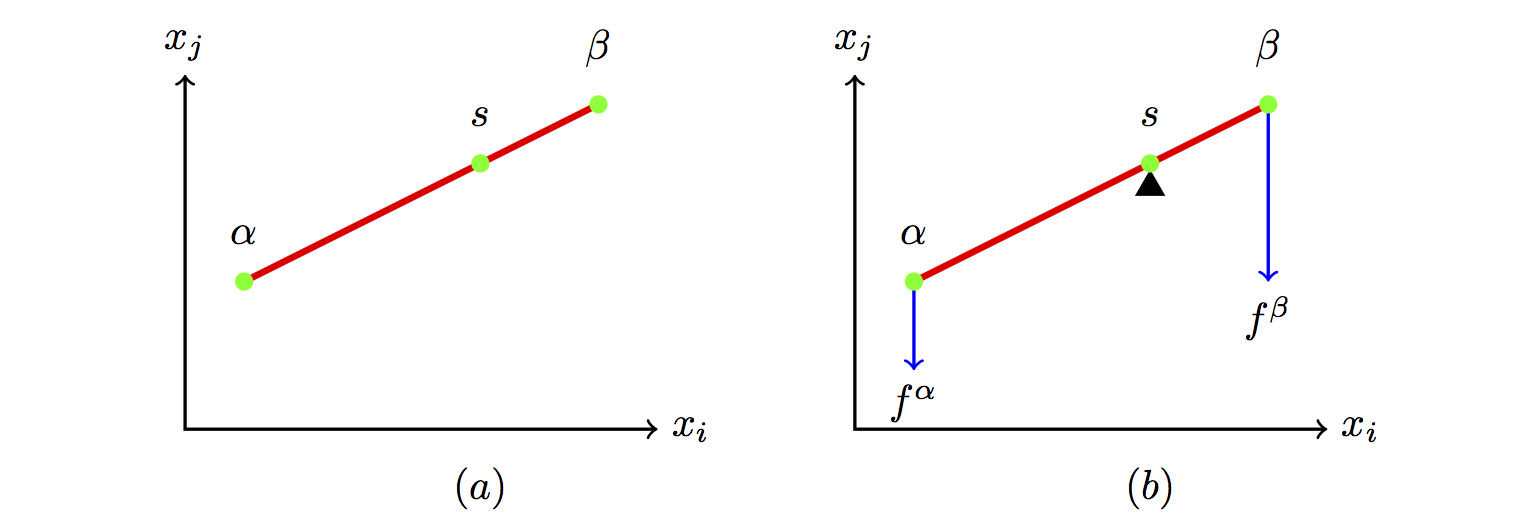
图 1: 两相平衡杠杆原理示意图
2. 三相平衡
假设一个平衡体系中有三个相:\(\alpha\)、\(\beta\)和\(\gamma\)。体系的组成与各个相的组成之间的关系是
\begin{align}
&x_i^{s} = f^{\alpha} x_i^{\alpha} + f^{\beta} x_i^{\beta} + f^{\gamma} x_i^{\gamma} \quad \quad (i=1,2,\cdots,c) \label{EQ8} \\
&f^{\alpha} + f^{\beta} + f^{\gamma}= 1 \label{EQ9}
\end{align}
式(\ref{EQ8})包含\(c\)个方程,至少有两个是相互独立的。假设在式(\ref{EQ8})中,组元是\(i\)和\(j\)的组成是相互独立的,那么我们就有下面的方程,
\begin{align}
&x_i^{s} = f^{\alpha} x_i^{\alpha} + f^{\beta} x_i^{\beta}+ f^{\gamma} x_i^{\gamma} \quad \quad (i=1,2,\cdots,c) \label{EQ10} \\
&x_j^{s} = f^{\alpha} x_j^{\alpha} + f^{\beta} x_j^{\beta} + f^{\gamma} x_j^{\gamma} \quad \quad (j=1,2,\cdots,c;j \neq i) \label{EQ11} \\
&f^{\alpha} + f^{\beta} + f^{\gamma}= 1 \label{EQ12}
\end{align}
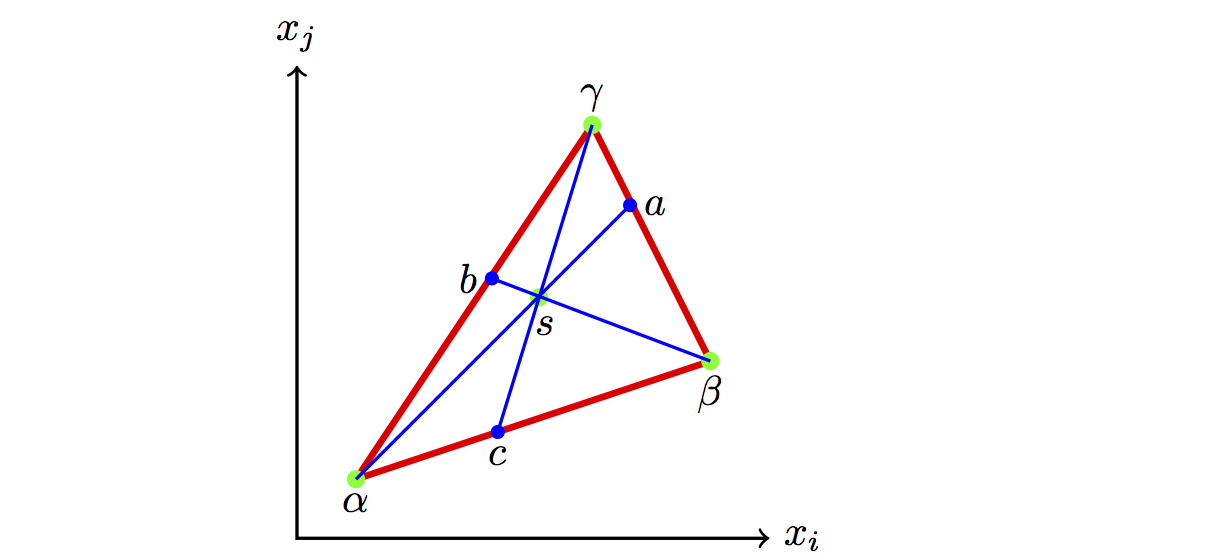
图 2: 三相平衡杠杆原理示意图
图2表明在二维组成空间 \(x_i\)-\(x_j\)中,体系总的组成点 \(s\)以及三个相 \(\alpha\)、\(\beta\)和\(\gamma\) 的组成点的示意图。\(s\)点位于三个相的组成点\(\alpha\)、\(\beta\)和\(\gamma\) 构成的三角形 \(\Delta _{\alpha \beta \gamma}\)的中间。 三角形 \(\Delta _{\alpha \beta \gamma}\)的三个顶点 \(\alpha\)、\(\beta\)和\(\gamma\)与\(s\)点的连线分别与三角形的边交于\(a\)、\(b\)和\(c\)。式(\ref{EQ10})-(\ref{EQ12})的解是
\begin{align}
f^{\alpha} = \frac {\Delta ^{\alpha}} {\Delta} \label{EQ13} \\
f^{\beta} = \frac {\Delta ^{\beta}} {\Delta} \label{EQ14} \\
f^{\gamma} = \frac {\Delta ^{\gamma}} {\Delta} \label{EQ15}
\end{align}
其中
\begin{align}
\Delta &=
\begin{array} {|ccc|}
x_i^{\alpha} & x_i^{\beta} & x_i^{\gamma}\\
x_j^{\alpha} & x_j^{\beta} & x_j^{\gamma}\\
1 & 1 & 1
\end{array} \label{EQ16} \\
\Delta ^{\alpha} &=
\begin{array} {|ccc|}
x_i^{s} & x_i^{\beta} & x_i^{\gamma}\\
x_j^{s} & x_j^{\beta} & x_j^{\gamma}\\
1 & 1 & 1
\end{array} \label{EQ17} \\
\Delta ^{\beta}&=
\begin{array} {|ccc|}
x_i^{\alpha} & x_i^{s} & x_i^{\gamma}\\
x_j^{\alpha} & x_j^{s} & x_j^{\gamma}\\
1 & 1 & 1
\end{array} \label{EQ18} \\
\Delta ^{\gamma}&=
\begin{array} {|ccc|}
x_i^{\alpha} & x_i^{\beta} & x_i^{s}\\
x_j^{\alpha} & x_j^{\beta} & x_j^{s}\\
1 & 1 & 1
\end{array} \label{EQ19}
\end{align}
根据解析几何的知识,我们知道,这里的\(\Delta\),\(\Delta ^{\alpha}\),\(\Delta ^{\beta}\),以及 \(\Delta ^{\gamma}\)都和三角形的面积有关,它们的关系是
\begin{align}
&\Delta \;\;=2 S_{\alpha \beta \gamma} \label{EQ20} \\
&\Delta ^{\alpha}=2 S_{s \beta \gamma} \label{EQ21} \\
&\Delta^{\beta}=2 S_{\alpha s \gamma} \label{EQ22} \\
&\Delta^{\gamma}=2 S_{\alpha \beta s} \label{EQ23}
\end{align}
这里\(S_{\alpha \beta \gamma}\)、\(S_{s \beta \gamma}\)、\(S_{\alpha s \gamma}\)和\(S_{\alpha \beta s}\)分别代表它们的下标三个点在图2中构成的三角形的面积。因此,每个相的相分数也可以用图2中相应的三角形的面积比来表示,
\begin{align}
&f^{\alpha} = \frac {S_{s \beta \gamma}} {S_{\alpha \beta \gamma}} \label{EQ24} \\
&f^{\beta} = \frac {S_{\alpha s \gamma}} {S_{\alpha \beta \gamma}} \label{EQ25} \\
&f^{\gamma} = \frac {S_{\alpha \beta s}} {S_{\alpha \beta \gamma}} \label{EQ26}
\end{align}
又因为三角形的面积比与相对应的线段比相等,相分数又可以表示成,
\begin{align}
&f^{\alpha} = \frac {\overline{s a}} {\overline{\alpha a}} \label{EQ27} \\
&f^{\beta} = \frac {\overline{s b}} {\overline{\beta b}} \label{EQ28} \\
&f^{\gamma} = \frac {\overline{s c}} {\overline{\gamma c}} \label{EQ29}
\end{align}
上面公式中的\(\overline{s a}\)代表点\(s\)和点\(a\)之间的距离,其余类推。
公式(\ref{EQ27})表示线段\(\overline{s a}\)与线段\(\overline{\alpha a}\)的比值是\(\alpha\)相的相分数\(f^{\alpha}\)。那么,线段\(\overline{\alpha s}\)与线段\(\overline{\alpha a}\)的比值又代表什么呢?上一节两相平衡的杠杆原理告诉我们,这个比值是\(f^{a}\),\(a\)点处的相分数,
\begin{align}
&f^{a} = \frac {\overline{\alpha s}} {\overline{\alpha a}} = 1 - f^{\alpha} = f^{\beta} + f^{\gamma} \label{EQ30}
\end{align}
因此,\(a\)点可以看作体系中除去\(\alpha\)相以外的其它的相的平均组成点,即\(\beta\) 和 \(\gamma\)相的平均组成,它的相分数是\(f^{\alpha}+f^{\gamma}\)。显然,\(a\)点处组成可以用两相的杠杆原理计算,
\begin{align}
&x_i^{a} = \frac {f^{\beta}} {f^{\beta}+f^{\gamma}} x_i^{\beta} + \frac {f^{\gamma}} {f^{\beta}+f^{\gamma}} x_i^{\gamma} \quad \quad (i=1,2,\cdots,c) \label{EQ30B}
\end{align}
体系在\(a\)点总的组成可以看作\(\alpha\)和\(a\)两个点的组成的加权平均,
\begin{align}
&x_i^{s}= f^{\alpha} x_i^{\alpha} + f^{a} x_i^{a} \quad \quad (i=1,2,\cdots,c) \label{EQ30C}
\end{align}
这种分析方法将有助于我们对凝固过程的理解。
3. 多相平衡
三相平衡的杠杆原理很容易推广到多相平衡中。假设一个平衡体系由\(p\)个相构成\((p\leq c)\)。每个相的组成是\(x_i^{(k)} (k=1,2,\cdots,p;i=1,2,\cdots,c)\)。从质量守恒和相的摩尔分数归一化,我们得到
\begin{align}
&x_i^{(s)} = \sum_{k=1}^{p} f^{(k)} x_i^{(k)} \quad \quad (i=1,2,\cdots,p-1) \label{EQ31} \\
&\sum_{k=1}^{p} f^{(k)} = 1 \label{EQ32}
\end{align}
这里取\(x_i (i=1,2,\cdots,p-1)\)作为相互独立的组成变量。定义
\begin{align}
\Delta &=
\begin{array} {|cccc|}
x_1^{(1)} & x_1^{(2)} & \cdots & x_1^{(p)}\\
x_2^{(1)} & x_2^{(2)} & \cdots & x_2^{(p)}\\
\vdots & \vdots & \ddots & \vdots \\
x_{p-1}^{(1)} & x_{p-1}^{(2)} & \cdots & x_{p-1}^{(p)}\\
1 & 1 & 1 & 1
\end{array} \label{EQ33} \\
\Delta^{(k)} &=
\begin{array} {|cccccccc|}
x_1^{(1)} & x_1^{(2)} & \cdots & x_1^{(k-1)} & x_1^{s} & x_1^{(k+1)} & \cdots & x_1^{(p)}\\
x_2^{(1)} & x_2^{(2)} & \cdots & x_2^{(k-1)} & x_2^{s} & x_2^{(k+1)} & \cdots & x_2^{(p)}\\
\vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\
x_{p-1}^{(1)} & x_{p-1}^{(2)} & \cdots & x_{p-1}^{(k-1)} & x_{p-1}^{s} & x_{p-1}^{(k+1)} & \cdots & x_{p-1}^{(p)}\\
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1
\end{array} \quad \quad (k=1,2,\cdots,p) \label{EQ34}
\end{align}
那么,体系中每个相的相分数可以由下式求得,
\begin{equation}
f^{(k)} = \frac {\Delta^{(k)}} {\Delta} \quad \quad (k=1,2,\cdots,p) \label{EQ35}
\end{equation}
式(\ref{EQ34})和式(\ref{EQ35})中的行列式与\(p\)-\(1\)维空间中\(p\)个点围成的体积有关,这里不再详细讨论。
4. 摩尔分数和质量分数
一个相的成份可以用组元的摩尔分数或质量分数来描述。它们之间的转换是通过组元的原子量或分子量进行的。
\(\alpha\)相中组元的摩尔分数(\(x_i^\alpha\))和质量分数(\(w_i^\alpha\))的关系是
\begin{align}
x_{i}^\alpha =\frac{ \frac {w_i^\alpha} {M_i}} {\sum\limits_{k=1}^{c} \frac {w_k^\alpha} {M_k}} \quad \quad (i=1,2,\cdots,c) \label{EQ36} \\
w_{i}^\alpha =\frac{ x_i^\alpha M_i} {\sum\limits_{k=1}^{c} x_k^\alpha M_k} \quad \quad (i=1,2,\cdots,c) \label{EQ37}
\end{align}
其中\(M_i\)代表组元\(i\)的原子量或分子量。定义\(\alpha\)相的分子量\(M^\alpha\)为
\begin{equation}
M^\alpha =\sum_{k=1}^{c} x_k^\alpha M_k \label{EQ37A}
\end{equation}
那么,式(\ref{EQ37})可写成
\begin{equation}
w_{i}^\alpha =\frac{ x_i^\alpha M_i} {M^\alpha} \quad \quad (i=1,2,\cdots,c) \label{EQ37B}
\end{equation}
在一个由多个相构成的体系中,每个相的相对量可以用它的相摩尔分数或相质量分数来描述。如果\(f^{(j)}\)代表第\(j\)个相的摩尔分数,\(f_w^{(j)}\)代表第\(j\)个相的质量分数,那么它们之间的关系是
\begin{align}
f^{(j)} =\frac{ \frac {f_w^{(j)}} {M^{(j)}}} {\sum\limits_{k=1}^{p} \frac {f_w^{(k)}} {M^{(k)}}} \quad \quad (j=1,2,\cdots,p) \label{EQ38} \\
f_w^{(j)} =\frac{ f^{(j)} M^{(j)}} {\sum\limits_{k=1}^{p} f^{(k)} M^{(k)}} \quad \quad (j=1,2,\cdots,p) \label{EQ39}
\end{align}
其中\(M^{(j)}\)代表第\(j\)相的分子量,\(p\)是体系中相的个数。
我们把表示多相平衡的杠杆原理的公式(\ref{EQ31})重新写在下面。对每一个组元\(i\),体系中组元\(i\)的平均摩尔分数为
\begin{equation}
x_i^{(s)} = \sum_{k=1}^{p} f^{(k)} x_i^{(k)} \quad \quad (i=1,2,\cdots,c) \label{EQ31A}
\end{equation}
两边乘以组元\(i\)的分子量\(M_i\)
\begin{equation}
x_i^{(s)}M_i = \sum_{k=1}^{p} f^{(k)} x_i^{(k)}M_i \quad \quad (i=1,2,\cdots,c) \label{EQ31B}
\end{equation}
对上式中的所有组元\(i\)求和,
\begin{equation}
\sum_{i=1}^{c}x_i^{(s)}M_i = \sum_{k=1}^{p} f^{(k)} \sum_{i=1}^{c} x_i^{(k)}M_i \label{EQ31C}
\end{equation}
用相的分子量\(M^{(k)}\)替代\(\sum\limits_{i=1}^{c}x_i^{(k)}M_i\),上式变成
\begin{equation}
M^{(s)}= \sum_{k=1}^{p} f^{(k)} M^{(k)} \label{EQ31D}
\end{equation}
即体系的总的分子量是各个相的分子量与相摩尔分数的加权平均。从式(\ref{EQ37B}),我们有
\begin{equation}
x_i^{(k)} M_i = w_{i}^{(k)} M^{(k)} \quad \quad (i=1,2,\cdots,c) \label{EQ37C}
\end{equation}
将上式代入式(\ref{EQ31B}), 我们得到
\begin{equation}
w_i^{(s)} M^{(s)}= \sum_{k=1}^{p}f^{(k)} w_i^{(k)} M^{(k)} \quad \quad (i=1,2,\cdots,c) \label{EQ37D}
\end{equation}
两边同除以\(M^{(s)}\),并运用式(\ref{EQ31D}),
\begin{align}
w_i^{(s)} &= \sum_{k=1}^{p} \frac{f^{(k)}M^{(k)}} {M^{(s)}} w_i^{(k)} \nonumber \\
&= \sum_{k=1}^{p} \frac{f^{(k)}M^{(k)}} {\sum\limits_{r=1}^{p} f^{(r)} M^{(r)}} w_i^{(k)} \quad \quad (i=1,2,\cdots,c) \label{EQ37E}
\end{align}
根据相的质量分数定义,公式(\ref{EQ39}),上式变成
\begin{equation}
w_i^{(s)} = \sum_{k=1}^{p} f_w^{(k)} w_i^{(k)} \quad \quad (i=1,2,\cdots,c) \label{EQ37F}
\end{equation}
这就是用质量分数表达的杠杆原理。 因此,质量分数表达的杠杆原理与摩尔分数表达的杠杆原理是一致的。
5. 摩尔分数空间和质量分数空间的对应关系
因为不同的组元有不同的分子量,所以相图中的相边界在摩尔分数空间和在质量分数空间是不完全一样的。但是,两个空间的点却是一一对应的,这可以从公式(\ref{EQ36})和(\ref{EQ37})看出:给定一组摩尔分数(\(x_i\)),存在唯一的一组质量分数(\(w_i\));给定一组质量分数(\(w_i\)),也有唯一的一组摩尔分数(\(x_i\))存在。两个空间中相对应的点处的不同组元\(i\)和\(j\)的摩尔分数和质量分数之间的关系是,
\begin{equation}
\frac{x_i M_i}{x_j M_j} =\frac{w_i}{w_j} \quad \quad (i,j=1,2,\cdots,c) \label{EQ40A}
\end{equation}
摩尔分数空间和质量分数空间的直线也是一一对应的。假设摩尔分数空间(\(x_i,i=1,2,\cdots,c\))中有一条直线。我们在这条直线上取三个不同的点,(\(x_i^{(s)},i=1,2,\cdots,c;s=1,2,3)\)。因为这三个点共线,它们满足杠杆原理,
\begin{equation}
x_i^{(3)} = f^{(1)} x_i^{(1)} + f^{(2)} x_i^{(2)} \quad \quad (i=1,2,\cdots,c) \label{EQ51}
\end{equation}
那么,在组元\(i\)、\(j\)和\(k\)组成的三维空间\((x_i, x_j, x_k)\)里,
\begin{align}
\begin {array} {|ccc|}
x_i^{(1)} & x_i^{(2)} & x_i^{(3)}\\
x_j^{(1)} & x_j^{(2)} & x_j^{(3)}\\
x_k^{(1)} & x_k^{(2)} & x_k^{(3)}
\end {array}
= &
\begin {array} {|ccc|}
x_i^{(1)} & x_i^{(2)} & x_i^{(3)}- f^{(1)} x_i^{(1)} - f^{(2)} x_i^{(2)}\\
x_j^{(1)} & x_j^{(2)} & x_j^{(3)}- f^{(1)} x_j^{(1)} - f^{(2)} x_j^{(2)}\\
x_k^{(1)} & x_k^{(2)} & x_k^{(3)}- f^{(1)} x_k^{(1)} - f^{(2)} x_k^{(2)}
\end {array} \nonumber \\
= &
\begin {array} {|ccc|}
x_i^{(1)} & x_i^{(2)} & 0\\
x_j^{(1)} & x_j^{(2)} & 0\\
x_k^{(1)} & x_k^{(2)} & 0
\end {array} \label{EQ52}
\end{align}
所以,
\begin{align}
\begin {array} {|ccc|}
x_i^{(1)} & x_i^{(2)} & x_i^{(3)}\\
x_j^{(1)} & x_j^{(2)} & x_j^{(3)}\\
x_k^{(1)} & x_k^{(2)} & x_k^{(3)}
\end {array}
= 0 \label{EQ53}
\end{align}
即,在摩尔分数空间\((x_i,x_j,x_k)\)中共线的三个点,它们的摩尔分数行列式的值为零。这是一个充分必要条件。
下面我们利用摩尔分数和质量分数之间的关系,公式(\ref{EQ40A}),推导上面三个点在质量分数空间的相对关系。
\begin{align}
\begin {array} {|ccc|}
x_i^{(1)} & x_i^{(2)} & x_i^{(3)}\\
x_j^{(1)} & x_j^{(2)} & x_j^{(3)}\\
x_k^{(1)} & x_k^{(2)} & x_k^{(3)}
\end {array}
=&
\frac{1}{M_i M_j} \begin {array} {|ccc|}
x_i^{(1)}M_i & x_i^{(2)}M_i & x_i^{(3)}M_i\\
x_j^{(1)}M_j & x_j^{(2)}M_j & x_j^{(3)}M_j\\
x_k^{(1)} & x_k^{(2)} & x_k^{(3)}
\end {array} \nonumber \\
=&
\frac{1}{M_i M_j} \begin {array} {|ccc|}
\frac{w_i^{(1)}}{w_k^{(1)}} x_k^{(1)}M_k &
\frac{w_i^{(2)}}{w_k^{(2)}} x_k^{(2)}M_k &
\frac{w_i^{(3)}}{w_k^{(3)}} x_k^{(3)}M_k \\
\frac{w_j^{(1)}}{w_k^{(1)}} x_k^{(1)}M_k &
\frac{w_j^{(2)}}{w_k^{(2)}} x_k^{(2)}M_k &
\frac{w_j^{(3)}}{w_k^{(3)}} x_k^{(3)}M_k \\
x_k^{(1)} & x_k^{(2)} & x_k^{(3)}
\end {array} \nonumber \\
=&
\frac{ x_k^{(1)} x_k^{(2)} x_k^{(3)}M_k M_k}{ w_k^{(1)} w_k^{(2)} w_k^{(3)} M_i M_j} \begin {array} {|ccc|}
w_i^{(1)} & w_i^{(2)} &w_i^{(3)} \\
w_j^{(1)} & w_j^{(2)} &w_j^{(3)} \\
w_k^{(1)} & w_k^{(2)} &w_k^{(3)}
\end {array} \nonumber \\
=& 0 \label{EQ54}
\end{align}
因此,
\begin{align}
\begin {array} {|ccc|}
w_i^{(1)} & w_i^{(2)} & w_i^{(3)}\\
w_j^{(1)} & w_j^{(2)} & w_j^{(3)}\\
w_k^{(1)} & w_k^{(2)} & w_k^{(3)}
\end {array}
= 0 \label{EQ55}
\end{align}
所以,在质量分数空间\((w_i,w_j,w_k)\)里,这三个点也是共线的。它们也满足质量分数的杠杆原理,
\begin{align}
w_i^{(3)} = f_w^{(1)} w_i^{(1)} + f_w^{(2)} w_i^{(2)} \quad \quad (i=1,2,\cdots,c) \label{EQ56}
\end{align}
由于组元\(i\)、\(j\)和\(k\)的选择是任意的,那么如果在摩尔分数空间,三个点满足杠杆原理,即共线,它们在质量分数空间里也一定满足杠杆原理,即共线。所以,摩尔分数空间中的直线和质量分数空间中的直线是一一对应的。换句话说,如果在摩尔分数空间里有三点共线,那么在质量分数空间里相应的三点也一定是共线的。
参考文献
1. L. S. Palatnik and A. I. Landau, Phase Equilibria in Multicomponent Systems, Holt, Rinehart and Winston, Inc., 1964.

