热力学与相图计算讲座
第二讲:标准态与参考态
热力学用能量来判断体系中相的相对稳定性。稳定是相对的。能量是绝对的,又是相对的。爱因斯坦的质能转化定律可以给出绝对的能量。一般来说,绝对能量的数值太大,不适用于热力学相平衡的计算。因此,我们定义一个标准的参考状态,简称为标准态(Standard State)。标准态的定义是:稳定单质元素在\(10^5Pa\)和298.15K时的焓值为零,\(H_{298.15K}=0\)(HSER:Enthalpy at Standard Element Reference);零度(T=0K)时熵为零,\(S_{0K}=0\)。根据这个标准态的定义,就可以计算各个稳定单质元素的Gibbs自由能与温度、压力的函数关系。Alan Dinsdale的文章[1]里给出了大多数元素的Gibbs自由能函数。 热力学、相平衡计算常用的函数是Gibbs自由能。根据标准态的定义,单质元素的Gibbs自由能函数值一般不会等于零。但我们可以任意选定一个状态(温度、压力以及相的结构)作为参考态,因为Gibbs自由能函数值也是相对的,只要保持体系中各个相Gibbs自由能之间的差值不随参考态的选择而变化就可以了。1. 元素的标准状态 (Standard Element Reference State)
元素的标准状态定义是:稳定单质元素在\(10^5Pa\)和298.15K时的焓值为零,零度(T=0K)是熵为零。用元素的热容对温度积分,可以得到不同温度下的焓\((H)\)和熵\((S)\)的值。然后利用\(G=H-TS\)就可以计算该元素在不同温度下的Gibbs自由能\((G)\)。要注意的是,元素磷(P)的标准态的定义比较特殊[1]。 图1和图2分别是元素铝和锌的液体和几种不同晶体结构的固体的Gibbs自由能随温度变化的曲线。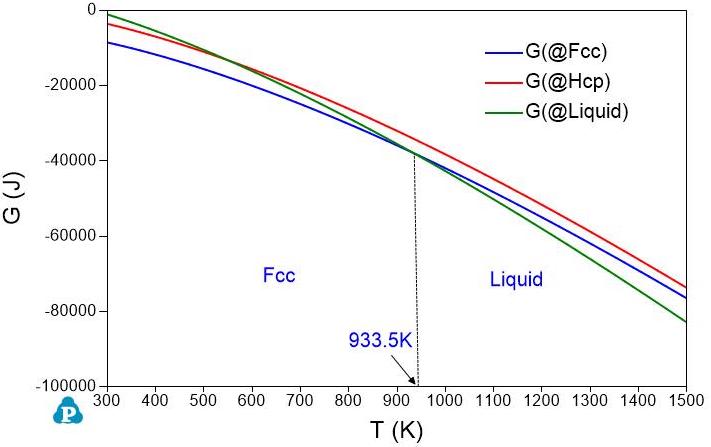
图 1: 铝的Gibbs自由能随温度变化图
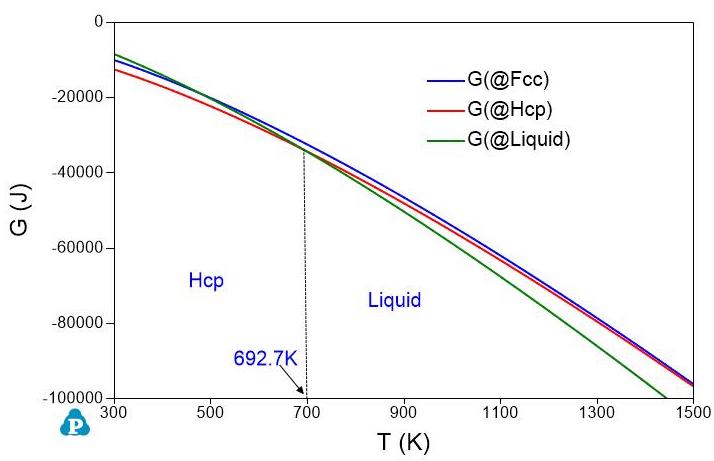
图 2: 锌的Gibbs自由能随温度变化图
2. 参考态(Reference State)
如果我们选取液相作为参考态,令\(G_{Al}^{Liquid}=0\)和\(G_{Zn}^{Liquid}=0\)。其它相的Gibbs自由能与液相Gibbs自由能之差保持不变。那么,图1和图2中的Gibbs自由能曲线就变成图3和图4中的Gibbs自由能曲线。虽然这几个相的Gibbs自由能值变了,但是同一个温度下不同相之间的Gibbs自由能差值不变,所以不同温度下的稳定的相是不变的。从图1或图3中,我们知道在温度低于\(933.5K\)时,Fcc相稳定;温度高于\(933.5K\)时,液相稳定。图2和图4表明Zn的Hcp结构在\(692.7K\)以下稳定,液体Zn在\(692.7K\)以上稳定。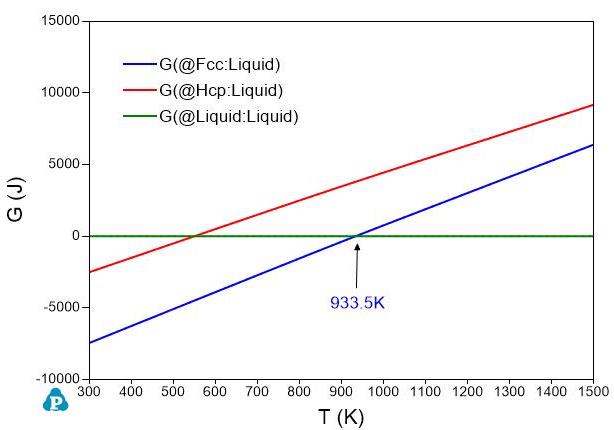
图 3: 铝的Gibbs自由能随温度变化图
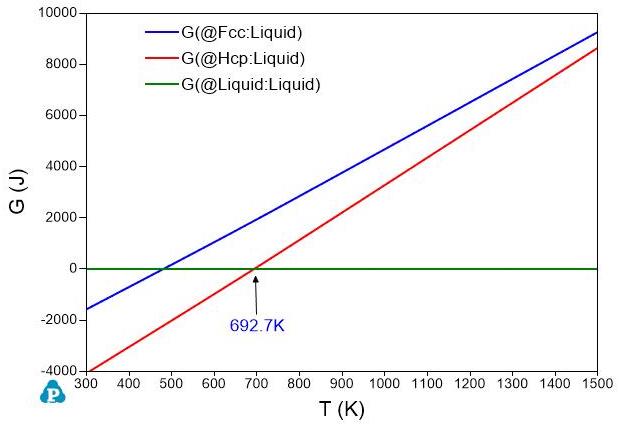
图 4: 锌的Gibbs自由能随温度变化图
3. 参考态与相平衡
相平衡由相之间的Gibbs自由能的相对值决定,不随参考态选择而变。 图5是Al-Zn二元系相图。\(800K\)下液体(Liquid)和Fcc相平衡,平衡组成分别为\(x_{Zn}^{Liquid}=0.4093\)和\(x_{Zn}^{Fcc}=0.1544\)。图6和图7分别是在\(800K\)下液体、Fcc以及Hcp相的Gibbs自由能曲线图。图6用的是元素的标准态,图7用的是液相的Al和Zn为参考态。虽然图6和图7中的Gibbs自由能值不同,但它们的平衡公切线的切点处的摩尔分数是完全一样的。因此,相的平衡状态与参考态的选择无关。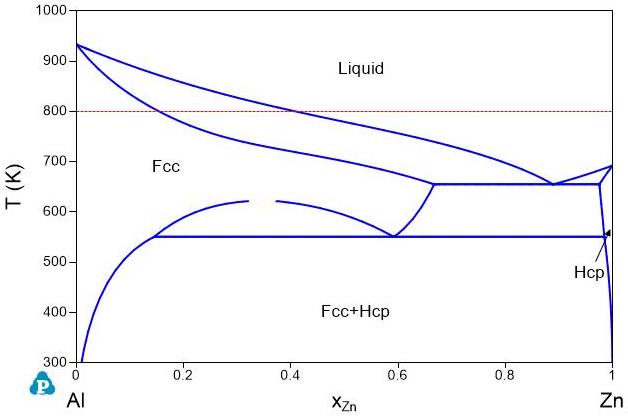
图 5: Al-Zn 二元相图
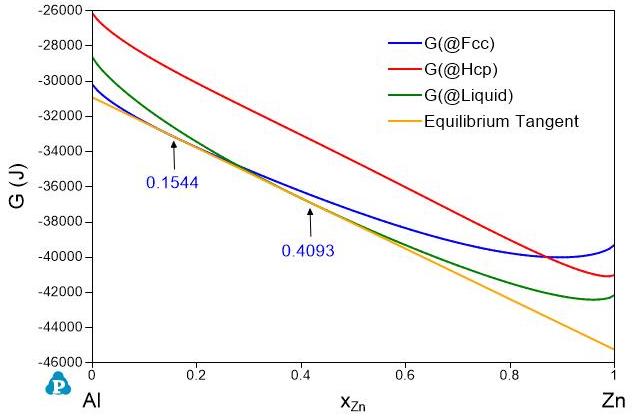
图 6: 800K下以元素的标准态计算的Gibbs自由能
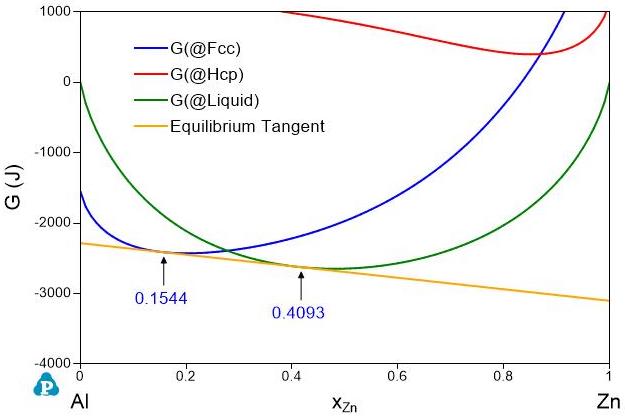
图 7: 800K下以液体的Al和Zn为参考态计算的Gibbs自由能